Innholdsfortegnelse:
Video: Hvordan løser du et lineært programmeringsproblem ved hjelp av hjørnemetoden?
2024 Forfatter: Miles Stephen | [email protected]. Sist endret: 2023-12-15 23:39
DE METODE FOR HJØRNER Tegn graf det mulige settet (region), S. Finn NØYE koordinater for alle toppunkter ( hjørne poeng) av S. Vurder objektivfunksjonen, P, ved hvert toppunkt Maksimum (hvis det finnes) er den største verdien av P ved et toppunkt. Minimum er den minste verdien av P ved et toppunkt.
Deretter kan man også spørre, hva er metodene for å løse LPP?
Grafisk metode for å løse lineære programmeringsproblemer
- Foreslåtte videoer.
- Trinn 1: Formuler LP-problemet (Lineær programmering).
- Trinn 2: Konstruer en graf og plott begrensningslinjene.
- Trinn 3: Bestem den gyldige siden av hver begrensningslinje.
- Trinn 4: Identifiser den mulige løsningsregionen.
- Trinn 5: Plott objektivfunksjonen på grafen.
- Trinn 6: Finn det optimale punktet.
hva er algebraisk metode i lineær programmering? Algebra og Simplex Metode . EN lineært programmeringsproblem (LP) er en optimaliseringsproblem der alle variabler er kontinuerlige, er målet en lineær (med hensyn til beslutningsvariablene) funksjon, og den gjennomførbare regionen er definert av et endelig antall lineær ulikheter eller ligninger.
Her, hvordan beregner du hjørnepunkter i lineær programmering?
De hjørnepunkter er toppunktene i den gjennomførbare regionen. Når du har grafen av systemet av lineær ulikheter, så kan du se på grafen og enkelt se hvor hjørnepunkter er. Du må kanskje løse et system av lineær ligninger til finne noen av koordinatene til poeng i midten.
Hva er hjørnepunktløsningsmetoden?
De hjørnepunktløsningsmetode består av fire nøkkeltrinn:: Bestem koordinatene til hvert toppunkt ( hjørnepunkt ) av den gjennomførbare regionen.: Beregn verdien av målfunksjonen ved hver hjørnepunkt .: Etabler målfunksjonen med maksimal verdi.
Anbefalt:
Hvordan måler du diameteren til en sylinder ved hjelp av en vernier caliper?
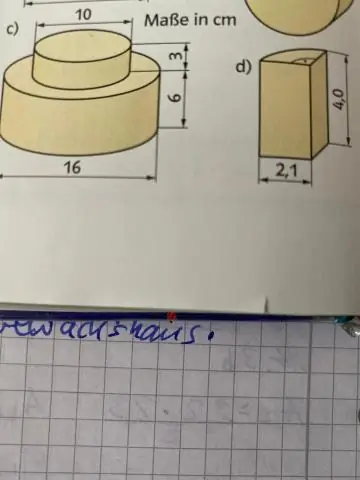
For å finne lengden på sylinderen/objektet: Hold sylinderen fra endene ved hjelp av de nedre kjevene på vernier-kaliperen. Legg merke til avlesningen på hovedskalaen som ligger like til venstre for nullmerket for nollskalaen. Se nå etter merket på vernier-skalaen som er på linje med et merke på hovedskalaen
Hvordan beregnes DNA-konsentrasjonen ved hjelp av spektrofotometer?
DNA-konsentrasjonen estimeres ved å måle absorbansen ved 260 nm, justere A260-målingen for turbiditet (målt ved absorbansen ved 320 nm), multiplisere med fortynningsfaktoren og bruke forholdet at en A260 på 1,0 = 50 µg/ml rent dsDNA
Hvordan finner du radiusen til en sirkel ved hjelp av pi?
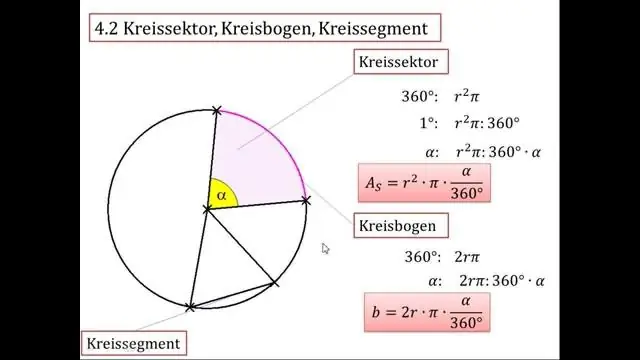
For å beregne radiusen til en sirkel ved å bruke omkretsen, tar du sirkelens omkrets og deler den med 2 ganger π. For en sirkel med en omkrets på 15, deler du 15 med 2 ganger 3,14 og runder av desimaltegnet til svaret ditt på omtrent 2,39
Hvordan kan du identifisere et metall ved hjelp av en flammetest?
Kjemikere bruker det samme prinsippet for å bestemme identiteten til ukjente metaller ved hjelp av en flammetest. Under en flammetest tar kjemikere et ukjent metall og legger det under en flamme. Flammen vil få forskjellige farger basert på hvilket metall som er i stoffet. Forskerne kan deretter identifisere deres ukjente stoff
Hvordan finner du motsatt side av en trekant ved hjelp av Pythagoras?
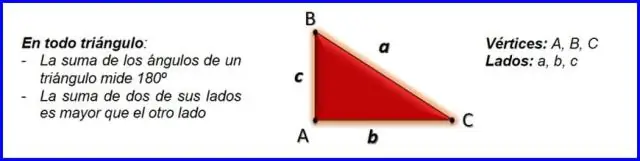
Rette trekanter og Pythagoras teorem Pythagoras teorem, a2+b2=c2, a 2 + b 2 = c 2, kan brukes til å finne lengden på en hvilken som helst side av en rettvinklet trekant. Siden motsatt den rette vinkelen kalles hypotenusen (side c på figuren)