
- Forfatter Miles Stephen [email protected].
- Public 2023-12-15 23:39.
- Sist endret 2025-06-01 05:05.
Bare tenk på en 2x2 matrise det er lik dens omvendte uten at de diagonale oppføringene er 1 eller -1. Diagonal matriser Vil gjøre. Så A og omvendt av A er lignende , så deres egenverdier er de samme. hvis en av As egenverdier er n, en egenverdi av dens omvendte vil være 1/n.
Også spurt, er en matrise lik dens transponering?
Hvilken som helst firkant matrise over et felt er ligner på transponeringen og ethvert kvadratisk kompleks matrise er lignende til et symmetrisk kompleks matrise.
Likeledes, er alle inverterbare matriser like? Hvis A og B er lignende og inverterbar , så er A-1 og B-1 lignende . Bevis. Siden alle de matriser er inverterbar , vi kan ta inversen av begge sider: B-1 = (P-1AP)-1 = P-1A-1(P-1)-1 = P-1A-1P, så A-1 og B-1 er lignende . Hvis A og B er lignende , så er Ak og Bk for enhver k = 1, 2,.
Angående dette, kan en matrise være lik seg selv?
Det vil si Any matrise er lik seg selv : I−1AI=A. Hvis A er lignende til B, så er B lignende til A: hvis B=P−1AP, så A=PBP−1=(P−1)−1BP−1. Hvis A er lignende til B via B=P−1AP, og C er lignende til B via C=Q−1BQ, så er A lignende til C: C=Q−1P−1APQ=(PQ)−1APQ.
Hva betyr det hvis matrisene er like?
I lineær algebra, to n-for-n matriser A og B kalles lignende hvis det finnes en inverterbar n-for-n matrise P slik at. Lignende matriser representere det samme lineære kartet under to (muligens) forskjellige baser, med P som endringen av basis matrise.
Anbefalt:
Hvordan forholder ordet matrise seg til mitokondrier?
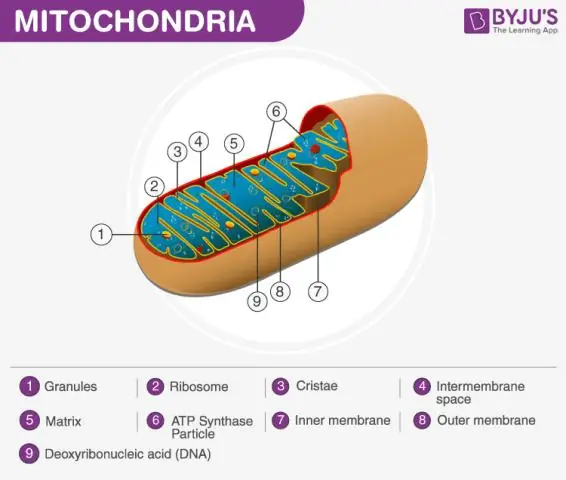
Mitokondriematrisen definert Mitokondriet består av en ytre membran, en indre membran og et gellignende materiale kalt matrisen. Denne matrisen er mer viskøs enn cellens cytoplasma da den inneholder mindre vann. Dette er et viktig trinn i cellulær respirasjon, som produserer energimolekyler kalt ATP
Hva er en vektor i matrise?
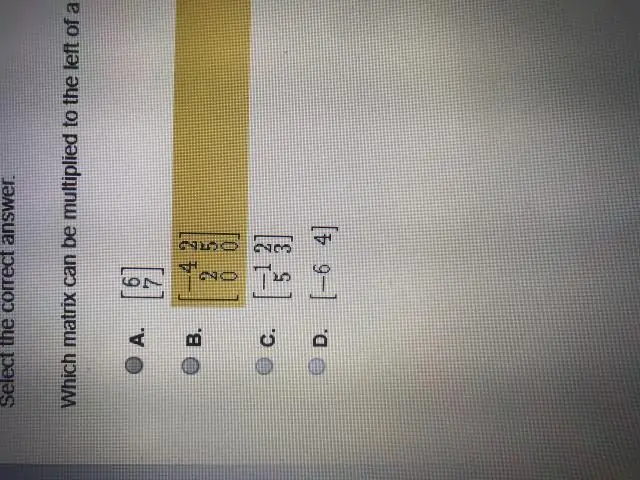
Skalarer, vektorer og matriser En skalar er et tall, som 3, -5, 0,368 osv. Avektor er en liste med tall (kan være i en rad eller kolonne), Amatrix er en rekke tall (en eller flere rader, én eller flere rader). flere kolonner)
Hvordan roterer du en 45 graders matrise?
Formelen for denne rotasjonen er: RM[x + y - 1][n - x + y] = M[x][y], der RM betyr rotert matrise, M den initiale matrisen og n dimensjonen til den initiale matrisen (som er nxn). Så, a32, fra den tredje raden og den andre kolonnen vil komme til den fjerde raden og den fjerde kolonnen
Hva er kanonisk matrise?

Kanonisk form. Teknikken som brukes til å representere de matematiske enhetene eller matrisen i sin standardform (eller matematiske uttrykk) kalles kanonisk form. Den trekantede formen, Jordan kanonisk form og rad echelon form er noen store kanoniske former i lineær algebra
Hvordan finner du den additive inverse av en matrise?

For å få additiv invers av gitt matrise, trenger vi bare å multiplisere hvert element i matrisen med -1. Når vi multipliserer hvert element i matrisen med -1, blir det lik -A. Derfor blir A+(-A) lik 0 der 0 er en nullmatrise. Den tilfredsstiller grunnleggende definisjon av additiv invers
