Video: Hvordan roterer du en 45 graders matrise?
2024 Forfatter: Miles Stephen | [email protected]. Sist endret: 2023-12-15 23:39
Formelen på dette rotasjon er: RM[x + y - 1][n - x + y] = M[x][y], der RM betyr rotert matrise , M initialen matrise , og n dimensjonen til initialen matrise (som er n x n). Så, a32, fra den tredje raden og den andre kolonnen vil komme til den fjerde raden og den fjerde kolonnen.
Følgelig, hvordan roterer du en 45 graders vinkel?
Hvis vi representerer punktet (x, y) med det komplekse tallet x+iy, så kan vi rotere den 45 grader med klokken ganske enkelt ved å multiplisere med det komplekse tallet (1−i)/√2 og deretter lese av x- og y-koordinatene deres.
Videre, hva er formlene for rotasjoner? 180 grader er (-a, -b) og 360 er (a, b). 360 grader endres ikke siden den er full rotasjon eller en hel sirkel. Også dette er for en mot klokken rotasjon . Hvis du vil gjøre en med klokken rotasjon følg disse formler : 90 = (b, -a); 180 = (-a, -b); 270 = (-b, a); 360 = (a, b).
hvordan roterer du en matrise 45 grader i Matlab?
RotateA = imrotate(A, 45 ); Det betyr at vi vil rotere datamatrise A av 45 grader og lagre den i array RotateA. Merk at rotasjon er i retning mot klokken rundt arrayets midtpunkt. Du kan angi en negativ verdi for vinkel til rotere bildet med klokken.
Hva er regelen for å rotere 90 grader mot klokken?
Generalen regel for rotasjon av en gjenstand 90 grader er (x, y) ------ (-y, x). Du kan bruke denne regel til rotere et forhåndsbilde ved å ta punktene til hvert toppunkt, oversette dem i henhold til regel , og tegner bildet.
Anbefalt:
Hvordan forholder ordet matrise seg til mitokondrier?
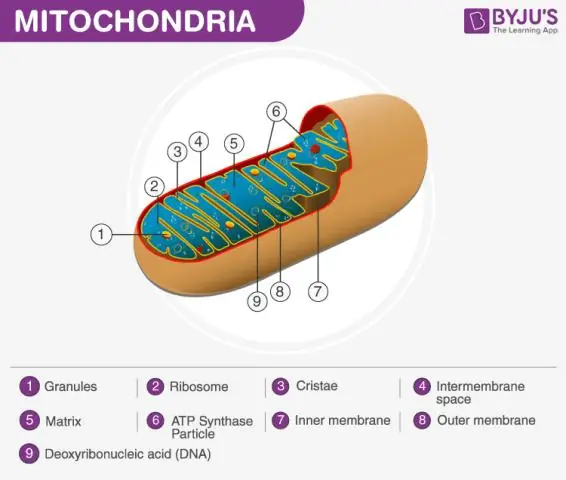
Mitokondriematrisen definert Mitokondriet består av en ytre membran, en indre membran og et gellignende materiale kalt matrisen. Denne matrisen er mer viskøs enn cellens cytoplasma da den inneholder mindre vann. Dette er et viktig trinn i cellulær respirasjon, som produserer energimolekyler kalt ATP
Hvordan gjør du en matrise til en identitetsmatrise?
VIDEO Dessuten, hvordan finner du inversen til en matrise ved å bruke en identitetsmatrise? Det fungerer på samme måte for matriser . Hvis du multipliserer a matrise (som A) og dens omvendt (i dette tilfellet A – 1 ), får du identitetsmatrise I.
Hvordan roterer du mot klokken?
Termer i dette settet (9) (-y, x) 90 graders rotasjon mot klokken rundt origo. (y, -x) 90 graders rotasjon med klokken rundt origo. (-x, -y) 180 graders rotasjon med klokken og mot klokken om origo. (-y, x) 270 graders rotasjon med klokken rundt origo. (y, -x) (x, -y) (-x, y) (y, x)
Hvordan finner du den additive inverse av en matrise?
For å få additiv invers av gitt matrise, trenger vi bare å multiplisere hvert element i matrisen med -1. Når vi multipliserer hvert element i matrisen med -1, blir det lik -A. Derfor blir A+(-A) lik 0 der 0 er en nullmatrise. Den tilfredsstiller grunnleggende definisjon av additiv invers
Hvordan beviser du at en matrise er et underrom?
Sentralisatoren til en matrise er et underrom La V være vektorrommet til n×n matriser, og M∈V en fast matrise. Definer W={A∈V∣AM=MA}. Settet W her kalles sentralisereren til M i V. Bevis at W er et underrom av V