Innholdsfortegnelse:
Video: Hvordan beviser du at en matrise er et underrom?
2024 Forfatter: Miles Stephen | [email protected]. Sist endret: 2023-12-15 23:39
Sentralisatoren til en Matrise er et underrom La V være vektorrom av n×n matriser , og M∈V a fast matrise . Definer W={A∈V∣AM=MA}. Settet W her kalles sentralisatoren til M i V. Bevise at W er en underrom av V.
Herav, hvordan beviser du et underrom?
For å vise et delsett er et delrom, må du vise tre ting:
- Vis den er stengt under tillegg.
- Vis at den er lukket under skalar multiplikasjon.
- Vis at vektoren 0 er i delmengden.
I tillegg, hva er grunnlaget for en matrise? Når vi ser etter basis av kjernen til en matrise , fjerner vi alle de redundante kolonnevektorene fra kjernen, og beholder de lineært uavhengige kolonnevektorene. Derfor, a basis er bare en kombinasjon av alle de lineært uavhengige vektorene.
Vet også, er identitetsmatrisen et underrom?
Spesielt identitetsmatrise i seg selv (1-er ned hoveddiagonalen, 0-er andre steder) er ikke en underrom av samlingen av 2×2 matriser , for hvis identitetsmatrise jeg er i underrom , da må cI være i underrom for alle tall c.
Hva er et underrom av en matrise?
EN underrom er et vektorrom som er inneholdt i et annet vektorrom. Så hver underrom er et vektorrom i seg selv, men det er også definert i forhold til et annet (større) vektorrom.
Anbefalt:
Hvordan forholder ordet matrise seg til mitokondrier?
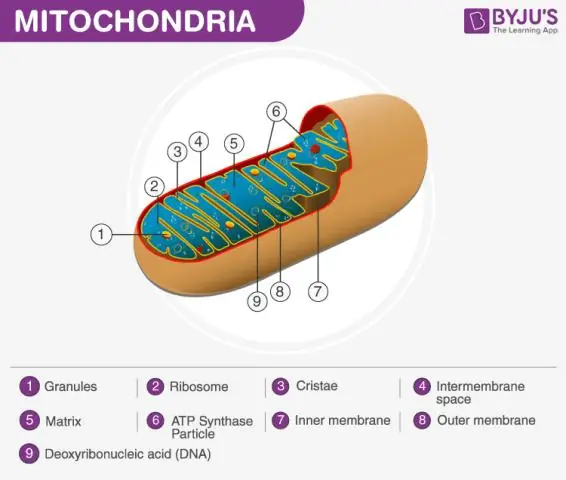
Mitokondriematrisen definert Mitokondriet består av en ytre membran, en indre membran og et gellignende materiale kalt matrisen. Denne matrisen er mer viskøs enn cellens cytoplasma da den inneholder mindre vann. Dette er et viktig trinn i cellulær respirasjon, som produserer energimolekyler kalt ATP
Er p2 et underrom av p3?
Ja! Siden hvert polynom med grad opp til 2 også er et polynom med grad opp til 3, er P2 en delmengde av P3. Og vi vet allerede at P2 er et vektorrom, så det er et underrom av P3. Det vil si at R2 ikke er en delmengde av R3
Hvordan roterer du en 45 graders matrise?
Formelen for denne rotasjonen er: RM[x + y - 1][n - x + y] = M[x][y], der RM betyr rotert matrise, M den initiale matrisen og n dimensjonen til den initiale matrisen (som er nxn). Så, a32, fra den tredje raden og den andre kolonnen vil komme til den fjerde raden og den fjerde kolonnen
Hvordan gjør du en matrise til en identitetsmatrise?
VIDEO Dessuten, hvordan finner du inversen til en matrise ved å bruke en identitetsmatrise? Det fungerer på samme måte for matriser . Hvis du multipliserer a matrise (som A) og dens omvendt (i dette tilfellet A – 1 ), får du identitetsmatrise I.
Hvordan finner du den additive inverse av en matrise?
For å få additiv invers av gitt matrise, trenger vi bare å multiplisere hvert element i matrisen med -1. Når vi multipliserer hvert element i matrisen med -1, blir det lik -A. Derfor blir A+(-A) lik 0 der 0 er en nullmatrise. Den tilfredsstiller grunnleggende definisjon av additiv invers