Innholdsfortegnelse:
Video: Hvordan løser du Tan-identiteter?
2024 Forfatter: Miles Stephen | [email protected]. Sist endret: 2023-12-15 23:39
For å bestemme forskjellsidentiteten for tangent, bruk det faktum at tan(−β) = −tanβ
- Eksempel 1: Finn den nøyaktige verdien av tan 75°.
- Eksempel 2: Bekreft det tan (180° − x) = − tan x.
- Eksempel 3: Bekreft det tan (180° + x) = tan x.
- Eksempel 4: Bekreft det tan (360° − x) = − tan x.
- Eksempel 5: Bekreft identitet .
Dessuten, hva er formelen for tangent?
I enhver rettvinklet trekant er tangent av en vinkel er lengden på motsatt side (O) delt på lengden på tilstøtende side (A). I en formel , skrives det ganske enkelt som 'tan'. Huskes ofte som "SOH" - som betyr at sinus er motsatt over hypotenusen.
I tillegg, hvordan omskriver du en tangent? Følg disse trinnene for å omskrive sinusfunksjonen når det gjelder tangent:
- Start med forholdsidentiteten som involverer sinus, cosinus og tangens, og multipliser hver side med cosinus for å få sinus alene til venstre.
- Erstatt cosinus med dens gjensidige funksjon.
- Løs den pytagoreiske identitetsbrunen2θ + 1 = sek2θ for sekant.
I denne forbindelse, hva er dobbeltvinkelformelen?
Om transkripsjon. Kosinus dobbeltvinkelformel forteller oss at cos(2θ) alltid er lik cos²θ-sin²θ. For eksempel er cos(60) lik cos²(30)-sin²(30). Vi kan bruke denne identiteten til å omskrive uttrykk eller løse problemer.
Hva er tangentidentiteten?
Summen identitet til tangent er utledet som følger: For å bestemme forskjellen identitet til tangent , bruk det faktum at tan (−β) = −tanβ. Den doble vinkelen identitet til tangent fås ved å bruke summen identitet til tangent . Halvvinkelen identitet til tangent kan skrives i tre forskjellige former.
Anbefalt:
Hvordan løser du en andregradsligning ved å bruke nullfaktorloven?
Fra dette kan vi slutte at: Hvis produktet av to tall er null, så er ett eller begge tallene null. Det vil si at hvis ab = 0, så er a = 0 eller b = 0 (som inkluderer muligheten for at a = b = 0). Dette kalles nullfaktorloven; og vi bruker det ofte til å løse andregradsligninger
Hvordan løser du Hardy Weinberg-problemer?
VIDEO Ved siden av dette, hvordan finner du P og Q i Hardy Weinberg? Siden s = 1 - q og q er kjent, er det mulig å beregne s også. Å vite p og q , er det en enkel sak å plugge disse verdiene inn i Hardy - Weinberg ligning (p² + 2pq + q² = 1).
Hvordan løser du ideell gasslov?
Ideal Gas Law Formel Spørsmål om ideal Gas Law Formel: Svar: Volumet er V = 890.0mL og temperaturen er T = 21°C og trykket er P = 750 mmHg. PV = nRT. Svar: Antall mol er n = 3,00 mol, temperaturen er T = 24°C og trykket er P = 762,4 mmHg. PV = nRT
Hvordan løser du tostegsligninger i prealgebra?
VIDEO På samme måte, hva er de 4 trinnene for å løse en ligning? En 4-trinns veiledning for å løse ligninger (del 2) Trinn 1: Forenkle hver side av ligningen. Som vi lærte sist, er det første trinnet i å løse en ligning å gjøre ligningen så enkel som mulig.
Hvordan løser du å multiplisere og dele brøker?
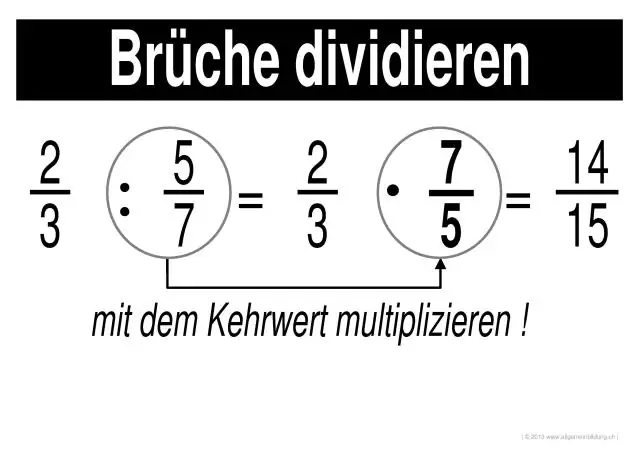
Multiplisere og dele brøker Trinn 1: Multipliser tellerne fra hver brøk med hverandre (tallene øverst). Resultatet er telleren for svaret. Trinn 2: Multipliser nevnerne til hver brøk med hverandre (tallene på bunnen). Resultatet er nevneren til svaret. Trinn 3: Forenkle eller reduser svaret