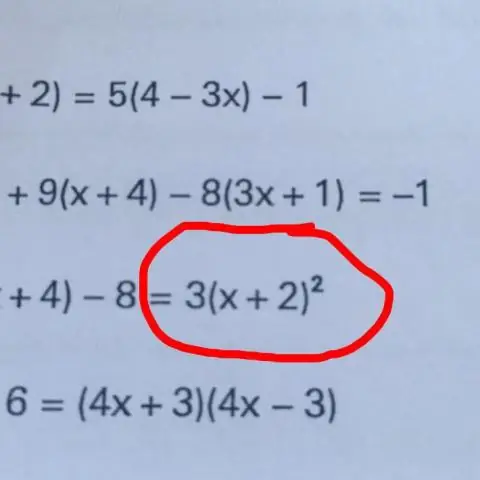
- Forfatter Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:39.
- Sist endret 2025-01-22 17:07.
Den grunnleggende teknikken til isolere en variabel er å "gjøre noe mot begge sider" av ligning , for eksempel addere, subtrahere, multiplisere eller dele begge sider av ligning med samme nummer. Ved å gjenta denne prosessen kan vi få variabel isolert på den ene siden av ligning.
Følgelig, hva er en formel i matematikk?
Definisjonen av en formel er en gruppe av matematisk symboler som uttrykker et forhold eller som brukes til å løse et problem, eller en måte å lage noe på. En gruppe av matte symboler som uttrykker forholdet mellom omkretsen av en sirkel og dens diameter er et eksempel på en formel.
På samme måte, hva mener du med variabel? I programmering, a variabel er en verdi som kan endres, avhengig av forhold eller informasjon som sendes til programmet. Vanligvis består et program av instruksjoner som forteller datamaskinen hva den skal gjøre og data som programmet bruker når det kjører.
På samme måte, hva er en bokstavelig ligning?
EN bokstavelig ligning er en ligning hvor variabler representerer kjente verdier. Bokstavelige ligninger tillate bruk for å representere ting som avstand, tid, interesse og helning som variabler i en ligning . Å bruke variabler i stedet for ord er en virkelig tidsbesparende!
Hva er koeffisienter?
I matematikk, a koeffisient er en multiplikasjonsfaktor i en eller annen term av et polynom, en serie eller et hvilket som helst uttrykk; det er vanligvis et tall, men kan være et hvilket som helst uttrykk. For eksempel, hvis y betraktes som en parameter i uttrykket ovenfor, vil koeffisient av x er −3y, og konstanten koeffisient er 1,5 + y.
Anbefalt:
Hvordan løser du en andregradsligning ved å bruke nullfaktorloven?

Fra dette kan vi slutte at: Hvis produktet av to tall er null, så er ett eller begge tallene null. Det vil si at hvis ab = 0, så er a = 0 eller b = 0 (som inkluderer muligheten for at a = b = 0). Dette kalles nullfaktorloven; og vi bruker det ofte til å løse andregradsligninger
Hvordan løser man et system med tre ligninger ved å eliminere?

Velg et annet sett med to ligninger, si ligningene (2) og (3), og eliminer den samme variabelen. Løs systemet skapt av ligningene (4) og (5). Bytt ut z = 3 i ligning (4) for å finne y. Bruk svarene fra trinn 4 og bytt inn i en hvilken som helst ligning som involverer den gjenværende variabelen
Hvordan løser du koeffisienten ved å fullføre kvadratet?

Nå kan vi løse en kvadratisk ligning i 5 trinn: Trinn 1 Del alle ledd med a (koeffisienten til x2). Trinn 2 Flytt tallleddet (c/a) til høyre side av ligningen. Trinn 3 Fullfør kvadratet på venstre side av ligningen og balanser dette ved å legge til samme verdi på høyre side av ligningen
Hvordan løser du et lineært programmeringsproblem ved hjelp av hjørnemetoden?
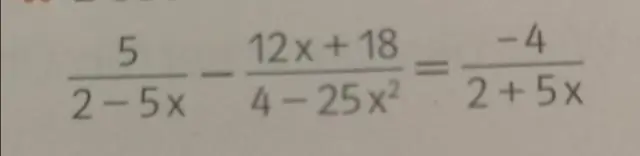
HJØRNEMETODEN Tegn grafen for det mulige settet (regionen), S. Finn de NØYAKTIGE koordinatene til alle toppunktene (hjørnepunkter) til S. Vurder objektivfunksjonen, P, ved hvert toppunkt Maksimum (hvis det finnes) er den største verdien av P ved et toppunkt. Minimum er den minste verdien av P ved et toppunkt
Hvordan løser du en lineær ligning ved å bruke Gauss eliminering?

Hvordan bruke gaussisk eliminering for å løse ligningssystemer Du kan multiplisere en hvilken som helst rad med en konstant (annet enn null). multipliserer rad tre med –2 for å gi deg en ny rad tre. Du kan bytte hvilke som helst to rader. bytter rad én og to. Du kan legge til to rader sammen. legger til rad én og to og skriver den i rad to
