
- Forfatter Miles Stephen [email protected].
- Public 2023-12-15 23:39.
- Sist endret 2025-06-01 05:05.
De restsetningen sier at f(a) er rest når polynomet f(x) er delt på x - a. Gitt et polynom, f(x), for å se om et lineært binomium på formen x - a er en faktor av polynomet løser vi for f(a). Hvis f(a) = 0, så er x - a a faktor , og x - a er ikke a faktor ellers.
På samme måte spørs det, hvordan fungerer restsetningen?
De restsetningen sier følgende: Hvis du deler et polynom f(x) med (x - h), så er det rest er f(h). De teorem slår fast at vår rest er lik f(h). Derfor, vi gjøre trenger ikke å bruke lang divisjon, men trenger bare å evaluere polynomet når x = h for å finne rest.
Man kan også spørre seg, hva betyr en rest av 0? Hvis x - c er en faktor, kan du skrive om det opprinnelige polynomet som (x - c) (kvotient). Du kan bruke syntetisk divisjon for å hjelpe deg med denne typen problemer. De Rest Teorem sier at f(c) = den rest . Så hvis rest kommer ut for å være 0 når du bruker syntetisk divisjon, så er x - c en faktor av f(x).
Videre, hva er poenget med Remainder Theorem?
De Resten teorem sier at vi kan omformulere polynomet i form av divisor, og deretter evaluere polynomet ved x = a. Men når x = a, er faktoren "x - a" bare null!
Er null en rest?
Når ett ledd ("utbytte") deles med et annet ledd ("deler"), er resultatet en "kvotient" og en " rest ". Når resten er null , både kvotient og divisor er faktorer for utbyttet. 0 er rest . Siden resten er null , både 2 og 3 er faktorer på 6.
Anbefalt:
Hvorfor fungerer Oobleck som et fast stoff og flytende?

Oobleck er en ikke-newtonsk væske, en betegnelse på væsker som endrer viskositet (hvor lett de flyter) under stress. Denne frastøtende kraften hjelper slurryen til å flyte, da partiklene foretrekker et lag med væske mellom da. Men når de presses sammen, tar friksjonen over og partiklene beveger seg som et fast stoff
Hvorfor fungerer en buffer best ved en pH nær pKa?
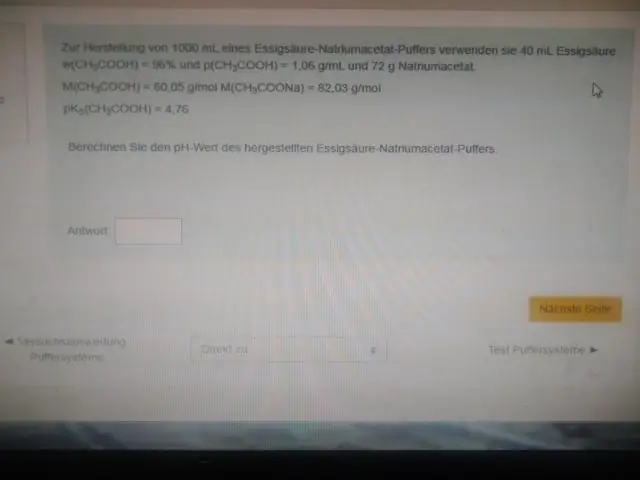
Med andre ord er pH i den ekvimolare løsningen av syre (f.eks. når forholdet mellom konsentrasjonen av syre og konjugatbase er 1:1) lik pKa. Denne regionen er den mest effektive for å motstå store endringer i pH når enten syre eller base tilsettes. En titreringskurve viser visuelt bufferkapasitet
Hvorfor fungerer prinsippet om lateral kontinuitet?

Prinsippet om lateral kontinuitet sier at lag med sediment i utgangspunktet strekker seg sideveis i alle retninger; med andre ord, de er sideveis kontinuerlige. Som et resultat kan bergarter som ellers ligner, men som nå er adskilt av en dal eller annet erosjonstrekk, antas å være opprinnelig sammenhengende
Hvorfor fungerer Archimedes-prinsippet?

Hvis flytekraften er større enn objektets vekt, vil objektet stige til overflaten og flyte. Arkimedes prinsipp sier at flytekraften på en gjenstand er lik vekten av væsken den fortrenger. Egenvekt er forholdet mellom tettheten til et objekt og en væske (vanligvis vann)
Hvorfor fungerer enzymer bare med spesifikke substrater?

Svar og forklaring: Enzymer fungerer bare med spesifikke substrater fordi hvert substrat har en unik 3-dimensjonal form
