Video: Kan summen av en aritmetisk rekke være negativ?
2024 Forfatter: Miles Stephen | [email protected]. Sist endret: 2023-12-15 23:39
Oppførselen til aritmetisk rekkefølge avhenger av felles forskjell d. Hvis den vanlige forskjellen, d, er: Positiv, den sekvens vil fremgang mot det uendelige (+∞) Negativ , den sekvens vil regress mot negativ uendelig (−∞)
Dessuten, kan summen av en serie være negativ?
Du snakker om sum av en uendelig serie som innebærer at serie er geometrisk, siden en uendelig aritmetikk serie kan aldri konvergere. Husk at det vanlige forholdet må være |r| < 1 for en sum å eksistere. Altså hvis fellesforholdet er positivt der kan være nei negativ sum.
Dessuten, hva er summen av endelige aritmetiske rekker? De sum av (n) vilkår for en aritmetiske serier er (5{n}^{2}-11n) for alle verdiene av (n). Bestem den felles forskjellen. De sum av en aritmetiske serier er (ext{100}) ganger første ledd, mens siste ledd er (ext{9}) ganger første ledd.
Derav, hvordan finner du summen av en aritmetisk serie?
Til finne de sum av en aritmetikk sekvens, start med å identifisere det første og siste tallet i sekvensen. Legg deretter disse tallene sammen og del sum med 2. Gang til slutt dette tallet med det totale antallet ledd i sekvensen til finne de sum.
Hva er N i serien?
Det første leddet er en1, den vanlige forskjellen er d, og antall ledd er. Summen av en aritmetikk serie finnes ved å multiplisere antall ledd ganger gjennomsnittet av første og siste ledd. For å finne, bruk den eksplisitte formelen for en aritmetikk sekvens . Vi løser 3 + (– 1)·4 = 99 for å få = 25.
Anbefalt:
Hva skjer når fysiologisk tetthet er høyere enn aritmetisk tetthet?
Den fysiologiske tettheten eller reell befolkningstetthet er antall mennesker per arealenhet dyrkbar mark. En høyere fysiologisk tetthet antyder at det tilgjengelige jordbruksarealet blir brukt av flere og kan nå produksjonsgrensen raskere enn et land som har lavere fysiologisk tetthet
Kan chi kvadrat være negativt?
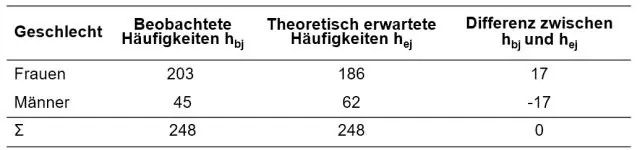
Mener du: Kan verdier av chi kvadrat noen gang være negative? Svaret er nei. Verdien av et chi-kvadrat kan ikke være negativt fordi det er basert på summen av kvadratiske forskjeller (mellom oppnådde og forventede resultater)
Kan en negativ og positiv stigning være parallell?
Teorem 104: Hvis to linjer har samme helning, så er linjene ikke-vertikale parallelle linjer. Hvis to linjer er vinkelrette og ingen av dem er vertikale, så har en av linjene en positiv helning, og den andre har en negativ helning. Dessuten er de absolutte verdiene til bakkene deres gjensidige
Hvordan finner du summen av en endelig aritmetisk eller geometrisk rekke?
Formelen for summen av n ledd i en geometrisk sekvens er gitt av Sn = a[(r^n - 1)/(r - 1)], der a er det første leddet, n er leddtallet og r er leddet felles forholdstall
Hvilken egenskap ved vann forklarer best dets evne til å løse opp en lang rekke materialer?
På grunn av sin polaritet og evne til å danne hydrogenbindinger, utgjør vann et utmerket løsningsmiddel, noe som betyr at det kan løse opp mange forskjellige typer molekyler