
- Forfatter Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:39.
- Sist endret 2025-01-22 17:06.
Descartes sin tegnregel sier antallet positive røtter er lik endringer i tegn av f(x), eller er mindre enn det med et partall (så du fortsetter å trekke fra 2 til du får enten 1 eller 0). Derfor kan den forrige f(x) ha 2 eller 0 positive røtter . Negativ ekte røtter.
Folk spør også, hva forteller Descartes tegnregel deg om de virkelige røttene til polynomet?
Descartes ' regel av tegn. Descartes ' regel av tegnet er vant til fastslå antall ekte nuller av a polynom funksjon. Den forteller oss at antallet positive ekte nuller i en polynom funksjonen f(x) er lik eller mindre enn med et partall som antall endringer i koeffisientenes fortegnet.
Vet også, hvor mange reelle røtter har et polynom? Hvis vi teller røtter i henhold til deres mangfold (se The Factor Theorem), så: A polynom av grad n kan ha bare et partall færre enn n ekte røtter . Således, når vi teller multiplisitet, en kubikk polynom kan ha bare tre røtter eller en rot ; en kvadratisk polynom kan ha bare to røtter eller null røtter.
Herav, hva er en ekte null?
Ekte nuller . Husk at a ekte null er der en graf krysser eller berører x-aksen. Tenk på noen punkter langs x-aksen.
Hvor mange røtter har en ligning?
En kvadratisk ligning med reelle koeffisienter kan ha enten en eller to distinkte ekte røtter , eller to forskjellige komplekser røtter . I dette tilfellet bestemmer diskriminanten antallet og arten av røtter . Det er tre tilfeller: Hvis diskriminanten er positiv, er det to forskjellige røtter.
Anbefalt:
Hvordan løser du en andregradsligning ved å bruke nullfaktorloven?

Fra dette kan vi slutte at: Hvis produktet av to tall er null, så er ett eller begge tallene null. Det vil si at hvis ab = 0, så er a = 0 eller b = 0 (som inkluderer muligheten for at a = b = 0). Dette kalles nullfaktorloven; og vi bruker det ofte til å løse andregradsligninger
Hvordan finner du den omtrentlige prosentandelen ved å bruke den empiriske regelen?

Finne arealet under kurven fra x = 9 til x = 13. Den empiriske regelen eller 68-95-99,7 %-regelen gir den omtrentlige prosentandelen av data som faller innenfor ett standardavvik (68 %), to standardavvik (95 %) , og tre standardavvik (99,7 %) av gjennomsnittet
Hvordan løser du Descartes tegnregel?

Descartes' tegnregel forteller oss at vi da har nøyaktig 3 reelle positive nuller eller færre, men et oddetall av nuller. Derfor må vårt antall positive nuller da være enten 3 eller 1. Her kan vi se at vi har to endringer av fortegn, derfor har vi to negative nuller eller færre, men et partall med nuller
Hvordan finner du volum ved å bruke Avogadros lov?

Avogadros lov viser at det er en direkte sammenheng mellom antall mol av en gass og dens volum. Dette kan også vises ved hjelp av ligningen: V1/n1 = V2/n2. Hvis antall mol dobles, vil volumet dobles
Hvordan finner du gjennomsnittet ved å bruke Excel?
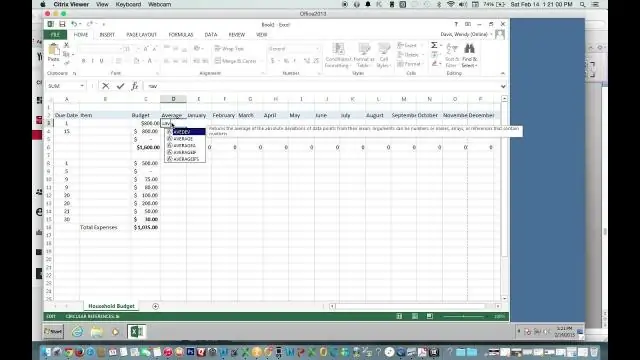
Bruk Autosum for raskt å finne gjennomsnittet Klikk på en celle under kolonnen eller til høyre for raden med tallene du vil finne gjennomsnittet for. På HJEM-fanen klikker du på pilen ved siden av Autosum > Gjennomsnitt, og trykker deretter på Enter
