- Forfatter Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:39.
- Sist endret 2025-01-22 17:07.
De domene av en funksjon er settet med alle mulige innganger for funksjon . For eksempel domene av f(x)=x² er alle reelle tall, og domene av g(x)=1/x er alle reelle tall bortsett fra x=0.
Herav, hvordan finner du domenet til en funksjon?
For denne typen funksjon , den domene er alle reelle tall. EN funksjon med en brøk med en variabel i nevneren. For å finne domene av denne typen funksjon , sett bunnen lik null og ekskluder x-verdien du finner når du løser ligningen. EN funksjon med en variabel inne i et radikalt tegn.
For det andre, hvordan finner du en funksjon på en graf? Den vertikale linjetesten kan brukes til å bestemme om en kurve representerer en funksjon . En vertikal linje inkluderer alle punkter med en bestemt x-verdi. y-verdien til et punkt der en vertikal linje skjærer a kurve representerer en utgang for den input x-verdien.
Dessuten, hvordan finner du domenet og rekkevidden til en funksjon?
En annen måte å identifisere domene og rekkevidde av funksjoner er ved å bruke grafer. Fordi det domene refererer til settet med mulige inngangsverdier, den domene av en graf består av alle inngangsverdiene vist på x-aksen. De område er settet med mulige utgangsverdier, som vises på y-aksen.
Hva er domenet i algebra?
De domene av en funksjon er det komplette settet med mulige verdier for den uavhengige variabelen. På vanlig engelsk betyr denne definisjonen: The domene er settet av alle mulige x-verdier som vil få funksjonen til å "fungere", og vil gi ut reelle y-verdier.
Anbefalt:
Hvordan bidrar strukturen til ATP til dens funksjon?
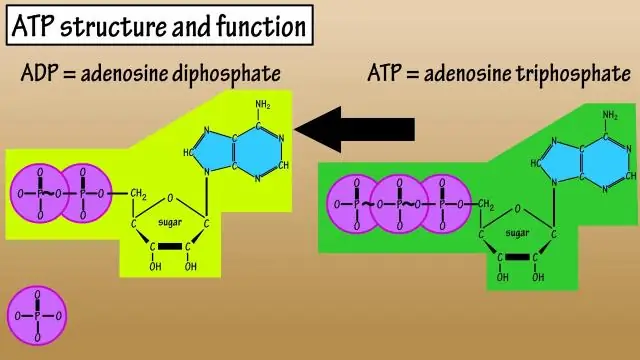
ATP fungerer som energivaluta for celler. Strukturen til ATP er den til et RNA-nukleotid med tre fosfater festet. Ettersom ATP brukes til energi, løsnes en fosfatgruppe eller to, og enten ADP eller AMP produseres. Energi avledet fra glukosekatabolisme brukes til å konvertere ADP til ATP
Hvordan vet du om en funksjon ikke er en funksjon?

Å avgjøre om en relasjon er en funksjon på en graf er relativt enkelt ved å bruke den vertikale linjetesten. Hvis en vertikal linje krysser relasjonen på grafen bare én gang alle steder, er relasjonen en funksjon. Men hvis en vertikal linje krysser relasjonen mer enn én gang, er relasjonen ikke en funksjon
Hvordan finner du røttene til en likning algebraisk?

Røttene til enhver kvadratisk ligning er gitt av: x = [-b +/- sqrt(-b^2 - 4ac)]/2a. Skriv ned kvadratet i form av ax^2 + bx + c = 0. Hvis ligningen er på formen y = ax^2 + bx +c, erstatt y-en med 0. Dette gjøres fordi røttene til ligningen er verdiene der y-aksen er lik 0
Hvordan finner du maksimalverdien til en kvadratisk funksjon?

Hvis du får formelen y = ax2 + bx + c, kan du finne maksimumsverdien ved å bruke formelen max =c- (b2 / 4a). Hvis du har ligningen y = a(x-h)2 + k og teaterm er negativ, så er maksimumsverdien k
Hvordan finner du domenet til en begrensning i en ligning?

Slik gjør du: Gitt en funksjon skrevet i en ligningsform som inkluderer en brøk, finn domenet. Identifiser inngangsverdiene. Identifiser eventuelle begrensninger på inngangen. Hvis det er en nevner i funksjonens formel, setter du nevneren lik null og løser for x
