Video: Hvordan vet du om en transformasjon er én til én?
2024 Forfatter: Miles Stephen | [email protected]. Sist endret: 2023-12-15 23:39
Når en lineær transformasjon er beskrevet i termen av en matrise er det lett å avgjøre om det lineære transformasjon er en-til-en eller ikke ved å sjekke den lineære avhengigheten til kolonnene i matrisen. Hvis kolonnene er lineært uavhengige, de lineære transformasjon er en-til-en.
I denne forbindelse, hva betyr det hvis en lineær transformasjon er én til én?
En-til-en lineære transformasjoner . Definisjon : A lineær transformasjon som kartlegger distinkte punkter/vektorer fra til distinkte punkter/vektorer i sies å være en en-til-en transformasjon eller et injeksjon transformasjon . For hver vektor eksisterer det altså nøyaktig en vektor slik at.
Man kan også spørre, kan en lineær transformasjon være på, men ikke én til én? I matrisetermer betyr dette at a transformasjon med matrise A er videre til hvis Ax=b har en løsning for hvilken som helst b i området. Hvis en transformasjon er på, men ikke en-til-en , du kan Tenk på at domenet har for mange vektorer til å passe inn i området.
Herav, kan en matrise være én til én og ikke på?
Spesielt den eneste matriser at kan være begge deler en-til-en og videre til er firkantede matriser . På den annen side, du kan ha an m×n matrise med m<n altså videre til , eller en det er ikke på . Og du kan har m×n matriser med m>n altså en-til-en , og matriser altså ikke en-til-en.
Hvordan beviser du en lineær transformasjon?
For hver y ∈ Y er det minst én x ∈ X med f(x) = y. Hvert element i codomenet til f er en utgang for noen input. Vi kan oppdage om a lineær transformasjon er en-til-en eller videre til ved å inspisere kolonnene i standardmatrisen (og radreduksjon).
Anbefalt:
Hvordan vet du om en transformasjon er en utvidelse?
En beskrivelse av en dilatasjon inkluderer skalafaktoren (eller forholdet) og midten av dilatasjonen. Utvidelsessenteret er et fast punkt i planet. Hvis skaleringsfaktoren er større enn 1, er bildet en forstørrelse (en strekk). Hvis skaleringsfaktoren er mellom 0 og 1, er bildet en reduksjon (en krymping)
Hvordan beskriver du transformasjon i bakterier?
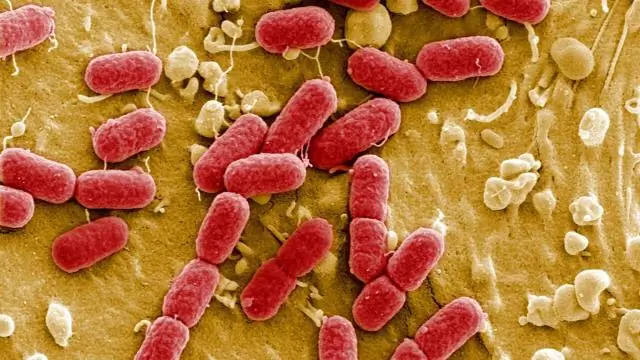
Biten av DNA eller genet av interesse kuttes fra sin opprinnelige DNA-kilde ved bruk av et restriksjonsenzym og limes deretter inn i plasmidet ved ligering. Plasmidet som inneholder det fremmede DNA er nå klart til å settes inn i bakterier. Denne prosessen kalles transformasjon
Hvordan bruker du transformasjon i en setning?
Transform setningseksempler Vi har aldri vært i stand til å forvandle en vamp til et menneske på tusenvis av år. Wesley trodde at Guds nåde kunne forvandle ethvert liv som mottok den. Politikken hennes har inntil i det siste vært å forvandle dem til fransk territorium
Hvordan bestemte Avery og hans gruppe hvilket molekyl som var viktigst for transformasjon?
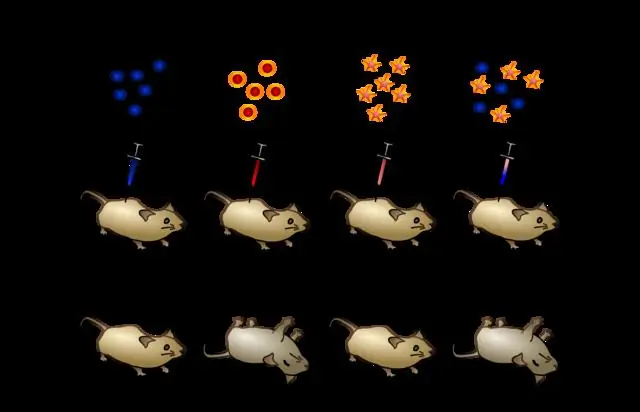
Beskriv kort hvordan Avery og gruppen hans bestemte hvilket molekyl som var viktigst for transformasjon. Avery og hans gruppe brukte to forskjellige enzymer på et ekstrakt av varmedrepte bakterier. Den ene ødela DNA, den andre ødela alt annet enn. De fant at transformasjon fortsatt skjedde når DNA var tilstede
Hvilken transformasjon vil endre figur A til figur B?
To figurer sies å være kongruente hvis den ene kan oppnås fra den andre ved en sekvens av translasjoner, refleksjoner og rotasjoner. Kongruente figurer har samme størrelse og form. For å transformere figur A til figur B, må du reflektere den over y-aksen og oversette en enhet til venstre