
- Forfatter Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:39.
- Sist endret 2025-01-22 17:06.
Så identitetsloven , p∧T≡p, betyr at konjunksjonen av enhver setning p med en vilkårlig tautologi T alltid vil ha samme sannhetsverdi som p (dvs. vil være logisk ekvivalent med p). Det betyr at disjunksjonen av enhver setning p med en vilkårlig tautologi T alltid vil være sann (vil i seg selv være en tautologi).
Også å vite er, hva er identitetsloven i matematikk?
An identitet er en likhet som gjelder uavhengig av verdiene som er valgt for variablene. For eksempel identitet (x + y) 2 = x 2 + 2 xy + y 2 (x+y)^2 = x^2 + 2xy + y^2 (x+y)2=x2+2xy+y2 er sant for alle valg av x og y, enten de er reelle eller komplekse tall.
Videre, hva er et eksempel på identitetsprinsipp? I logikken er loven om identitet sier at hver ting er identisk med seg selv. Det er den første av de tre tankelovene, sammen med loven om ikke-motsigelse, og loven om utelukket middel. Det kan også skrives mindre formelt ettersom A er A. En påstand om en slik prinsipp er "Rose er en rose er en rose er en rose."
Deretter kan man også spørre, hva er De Morgan-loven i diskret matematikk?
De Morgans lover beskriv hvordan matematisk utsagn og begreper henger sammen gjennom sine motsetninger. I settteori, De Morgans lover relatere skjæringspunktet og foreningen av sett gjennom komplementer. I proposisjonell logikk, De Morgans lover relatere konjunksjoner og disjunksjoner av proposisjoner gjennom negasjon.
Hva er diskrete matematiske implikasjoner?
Definisjon: La p og q være proposisjoner. Proposisjonen "p eller q" angitt med p ∨ q, er usann når både p og q er usann og er sann ellers. Proposisjonen "p innebærer q" angitt med p → q kalles implikasjon . Det er usant når p er sant og q er usant og er sant ellers.
Anbefalt:
Hva er meningen med diskret struktur?

Diskret struktur Et sett med diskrete elementer som visse operasjoner er definert på. Diskret innebærer ikke-kontinuerlige og derfor inkluderer diskrete sett endelige og tellbare mengder, men ikke utellelige mengder som de reelle tallene
Hva er matriser i diskret matematikk?
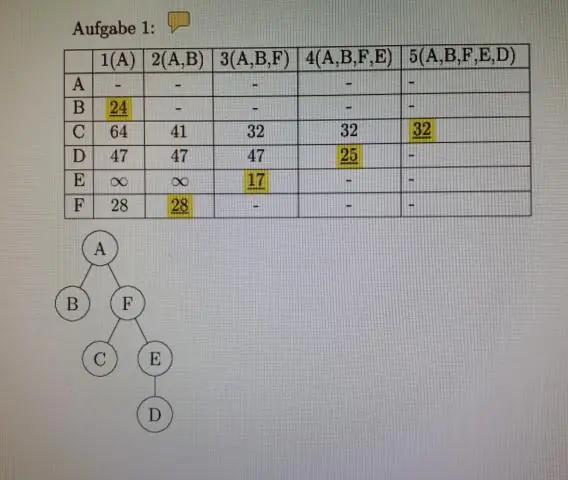
Diskret matematikk og dens anvendelser Kapittel 2 Notater 2.6 Matriser Forelesningslysbilder Av Adil Aslammailto:adilaslam5959@gmail.com. Definisjon av matrise •En matrise er en rektangulær matrise med tall. En matrise med m rader og n kolonner kalles en m x n matrise. Flertallet av matrise er matriser
Hva er diskret og kontinuerlig i statistikk?
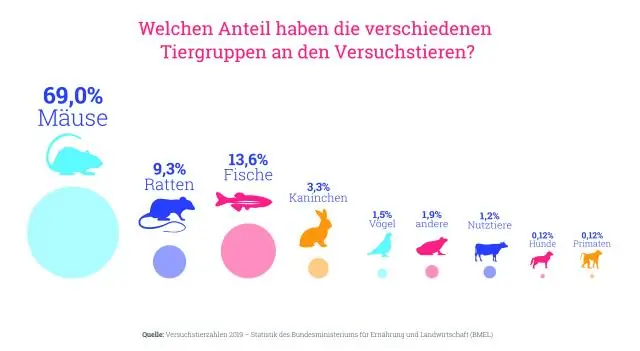
Kontinuerlige vs. diskrete distribusjoner. Kontrolldiagrammer: En diskret distribusjon er en der dataene bare kan anta visse verdier, for eksempel heltall. En kontinuerlig fordeling er en der data kan få en hvilken som helst verdi innenfor et spesifisert område (som kan være uendelig)
Hva er ekvivalens i diskret matematikk?
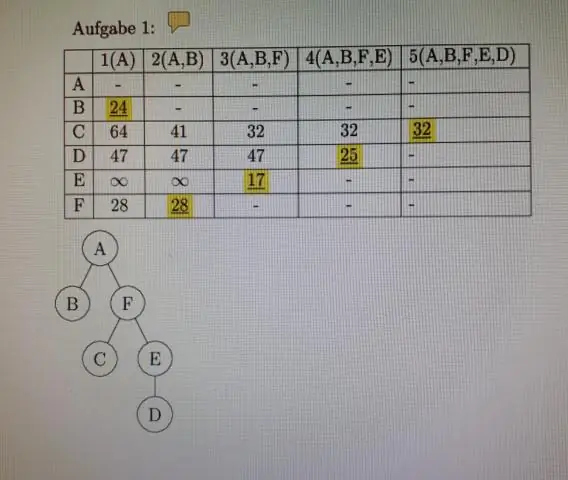
I matematikk er en ekvivalensrelasjon en binær relasjon som er refleksiv, symmetrisk og transitiv. Relasjonen 'er lik' er det kanoniske eksemplet på en ekvivalensrelasjon, der for alle objekter a, b og c: a = a (refleksiv egenskap), hvis a = b og b = c så a = c (transitiv egenskap). )
Hva er sett diskret matematikk?
Et sett er en uordnet samling av forskjellige elementer. Et sett kan skrives eksplisitt ved å liste opp elementene ved hjelp av settparentes. Hvis rekkefølgen på elementene endres eller et element i et sett gjentas, gjør det ingen endringer i settet
