Video: Hvordan løser du identitetseiendom?
2024 Forfatter: Miles Stephen | [email protected]. Sist endret: 2023-12-15 23:39
De Identitetseiendom består av to deler: Additiv Identitet og multiplikativ Identitet . Legg null (0) til et tall, summen er dette tallet. Multipliser et tall med 1, produktet er det tallet. Del et tall med seg selv, kvotienten er 1.
Spørsmålet er også, hva er et eksempel på identitetseiendom?
Om transkripsjon. De identitetseiendom av 1 sier at ethvert tall multiplisert med 1 beholder sitt identitet . Med andre ord, ethvert tall multiplisert med 1 forblir det samme. Grunnen til at tallet forblir det samme er fordi multiplisering med 1 betyr at vi har 1 kopi av tallet. Til eksempel , 32x1=32.
Foruten ovenfor, hvordan påvirker identitetsegenskapen tall? De identitetseiendom av addisjon sier at summen av a Nummer og null er Nummer . Hvis a er en ekte Nummer , så a+0=a. Det omvendte eiendom av tillegg sier at summen av enhver reell Nummer og dens additive invers (motsatt) er null. Hvis a er en ekte Nummer , deretter a+(-a)=0.
På samme måte spørs det, hva er identitetsegenskapen?
Identitetseiendom . De identitetseiendom for addisjon forteller oss at null lagt til et hvilket som helst tall er selve tallet. Null kalles "tilsetningsstoffet identitet ." Den identitetseiendom for multiplikasjon forteller oss at tallet 1 ganget med et hvilket som helst tall gir selve tallet.
Hva er identitetsegenskapen til 1?
I følge multiplikativen identitetseiendom til 1 , et hvilket som helst tall multiplisert med 1 , gir samme resultat som selve tallet. Det kalles også Identitetseiendom av multiplikasjon, fordi identitet av antallet forblir det samme. Her er noen eksempler på identitetseiendom av multiplikasjon.
Anbefalt:
Hvordan løser du en andregradsligning ved å bruke nullfaktorloven?
Fra dette kan vi slutte at: Hvis produktet av to tall er null, så er ett eller begge tallene null. Det vil si at hvis ab = 0, så er a = 0 eller b = 0 (som inkluderer muligheten for at a = b = 0). Dette kalles nullfaktorloven; og vi bruker det ofte til å løse andregradsligninger
Hvordan løser du Hardy Weinberg-problemer?
VIDEO Ved siden av dette, hvordan finner du P og Q i Hardy Weinberg? Siden s = 1 - q og q er kjent, er det mulig å beregne s også. Å vite p og q , er det en enkel sak å plugge disse verdiene inn i Hardy - Weinberg ligning (p² + 2pq + q² = 1).
Hvordan løser du ideell gasslov?
Ideal Gas Law Formel Spørsmål om ideal Gas Law Formel: Svar: Volumet er V = 890.0mL og temperaturen er T = 21°C og trykket er P = 750 mmHg. PV = nRT. Svar: Antall mol er n = 3,00 mol, temperaturen er T = 24°C og trykket er P = 762,4 mmHg. PV = nRT
Hvordan løser du tostegsligninger i prealgebra?
VIDEO På samme måte, hva er de 4 trinnene for å løse en ligning? En 4-trinns veiledning for å løse ligninger (del 2) Trinn 1: Forenkle hver side av ligningen. Som vi lærte sist, er det første trinnet i å løse en ligning å gjøre ligningen så enkel som mulig.
Hvordan løser du å multiplisere og dele brøker?
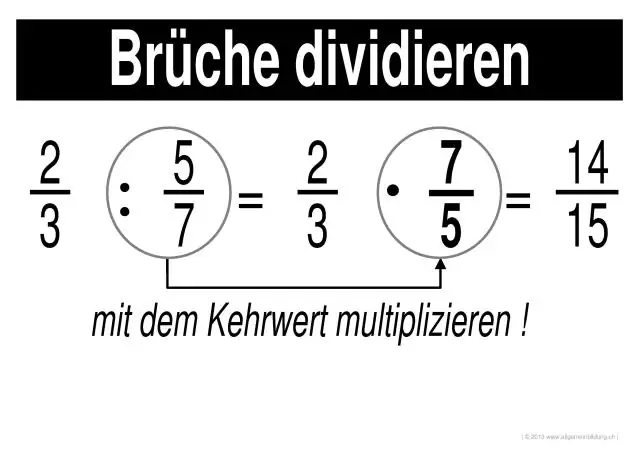
Multiplisere og dele brøker Trinn 1: Multipliser tellerne fra hver brøk med hverandre (tallene øverst). Resultatet er telleren for svaret. Trinn 2: Multipliser nevnerne til hver brøk med hverandre (tallene på bunnen). Resultatet er nevneren til svaret. Trinn 3: Forenkle eller reduser svaret