Video: Hvorfor har rasjonelle funksjoner begrensninger?
2024 Forfatter: Miles Stephen | [email protected]. Sist endret: 2023-12-15 23:39
Domene begrensninger av en rasjonell funksjon kan bestemmes ved å sette nevneren lik null og løse. x -verdiene der nevneren er lik null er kalt singulariteter og er ikke i domenet til funksjon.
På samme måte, hvorfor er rasjonelle funksjoner viktige?
Betydning. " Rasjonell funksjon " er navnet gitt til en funksjon som kan representeres som kvotienten av polynomer, akkurat som en rasjonell tall er et tall som kan uttrykkes som en kvotient av hele tall. Rasjonelle funksjoner forsyning viktig eksempler og forekommer naturlig i mange sammenhenger.
På samme måte har rasjonelle funksjoner vendepunkter? 4 Sammendrag. Et polynom av grad n har maksimalt n reelle nuller og n−1 vendepunkter . EN rasjonell funksjon er en funksjon av formen f(x)=P(x)Q(x), f (x) = P (x) Q (x), hvor P(x) og Q(x) er begge polynomene.
Spørsmålet er også, hva er et eksempel på rasjonell funksjon?
Eksempler av Rasjonelle funksjoner De funksjon R(x) = (x^2 + 4x - 1) / (3x^2 - 9x + 2) er en rasjonell funksjon siden telleren, x^2 + 4x - 1, er et polynom og nevneren, er 3x^2 - 9x + 2 også et polynom.
Hva kjennetegner rasjonelle funksjoner?
To viktige funksjoner av noen rasjonell funksjon r(x)=p(x)q(x) r (x) = p (x) q (x) er alle nuller og vertikale asymptoter funksjon kan ha. Disse aspektene ved en rasjonell funksjon er nært knyttet til hvor henholdsvis telleren og nevneren er null.
Anbefalt:
Hvorfor oppgir vi restriksjoner for rasjonelle uttrykk og når oppgir vi restriksjonene?
Vi oppgir restriksjoner fordi det kan føre til at ligningen er udefinert i noen verdier av x. Den vanligste begrensningen for rasjonelle uttrykk er N/0. Dette betyr at ethvert tall delt på null er udefinert. For eksempel, for funksjonen f(x) = 6/x², når du erstatter x=0, vil det resultere til 6/0 som er udefinert
Hvordan bruker jeg dimensjonale begrensninger i AutoCAD?
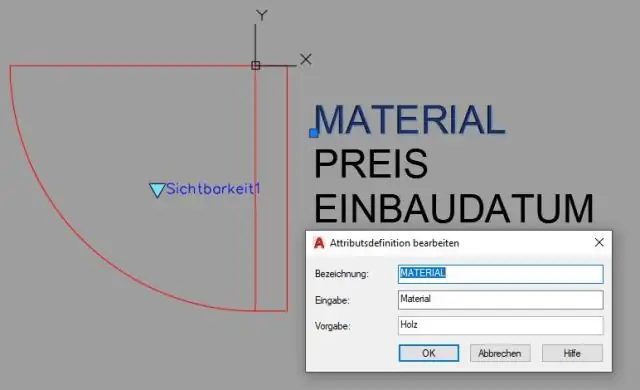
Disse trinnene presenterer et enkelt eksempel på dimensjonsbegrensninger: Start en ny tegning og gjør båndets Parametriske-fane oppdatert. Slå på passende presisjonstegningshjelpemidler på statuslinjen, for eksempel Snap, Ortho og Osnap. Tegn noen rimelig presis geometri ved å bruke en presisjonsteknikk
Hvilke funksjoner har nukleinsyrer?
Funksjonene til nukleinsyrer har å gjøre med lagring og uttrykk for genetisk informasjon. Deoksyribonukleinsyre (DNA) koder for informasjonen cellen trenger for å lage proteiner. En beslektet type nukleinsyre, kalt ribonukleinsyre (RNA), kommer i forskjellige molekylære former som deltar i proteinsyntesen
Hvorfor kalles trigonometriske funksjoner sirkulære funksjoner?
Trigonometriske funksjoner kalles noen ganger sirkulære funksjoner. Dette er fordi de to grunnleggende trigonometriske funksjonene – sinus og cosinus – er definert som koordinatene til et punkt P som beveger seg rundt på enhetssirkelen med radius 1. Sinus og cosinus gjentar sine utdata med jevne mellomrom
Hvordan multipliserer du rasjonelle funksjoner?
Q og S er ikke lik 0. Trinn 1: Faktor både telleren og nevneren. Trinn 2: Skriv som én brøk. Trinn 3: Forenkle det rasjonelle uttrykket. Trinn 4: Multipliser eventuelle gjenværende faktorer i telleren og/eller nevneren. Trinn 1: Faktor både telleren og nevneren. Trinn 2: Skriv som én brøk