2024 Forfatter: Miles Stephen | [email protected]. Sist endret: 2023-12-15 23:39
Det er en kombinasjon av to betingede uttalelser, "hvis to linjestykker er kongruente, så er de like lange" og "hvis to linjestykker er like lange, så er de kongruente". EN bibetinget er sant hvis og bare hvis begge betingelser er sanne. Bi- betingelser representeres av symbolet ↔ eller ⇔.
Videre, når kan du skrive en bibetinget erklæring?
Når du kombinere en betinget uttalelse og det motsatte, du lage en bibetinget uttalelse . EN bibetinget uttalelse er en uttalelse at kan skrives på formen "p hvis og bare hvis q." Dette betyr "hvis p, så q" og "hvis q, så p." De bibetinget "p hvis og bare hvis q" kan også skrives som "p iff q" eller p ? q.
Videre, er bare hvis en bibetinget? HVIS OG BARE HVIS , er en bibetinget påstand, som betyr at enten begge påstandene er sanne eller begge er usanne. Så det er i hovedsak og HVIS ” uttalelse som fungerer begge veier.
Også å vite, hva er betingede og bibetingede utsagn?
Når vi kombinerer to betingede uttalelser på denne måten har vi en bibetinget . Definisjon: A bibetinget uttalelse er definert til å være sann når begge deler har samme sannhetsverdi. I sannhetstabellen ovenfor er p q sann når p og q har samme sannhetsverdier, (dvs. når begge er sanne eller begge er usanne.)
Hva er et eksempel på en bibetinget uttalelse?
Eksempler på bibetinget erklæring De bibetingede uttalelser for disse to settene vil være: Polygonet har bare fire sider hvis og bare hvis polygonet er en firkant. Polygonet er en firkant hvis og bare hvis polygonet bare har fire sider.
Anbefalt:
Hvordan skriver du formelen for en forbindelse som inneholder et polyatomisk ion?
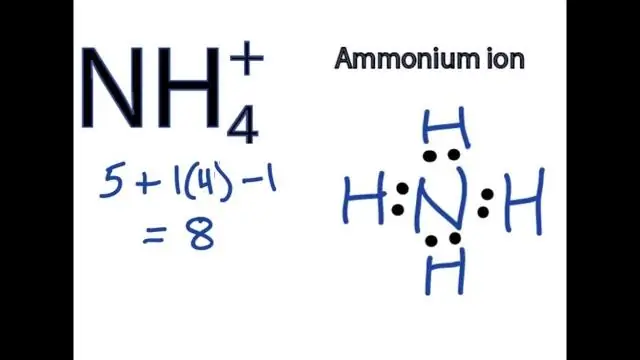
For å skrive formler for forbindelser som inneholder polyatomiske ioner, skriv symbolet for metallionet etterfulgt av formelen for det polyatomiske ionet og balanser ladningene. For å navngi en forbindelse som inneholder et polyatomisk ion, oppgi først kation og deretter anion
Hvordan skriver du 13/4 som et blandet tall?
Som en negativ uekte brøk (|teller| > |nevner|): - 13/4 = - 13/4 Som et blandet tall. (et helt tall og en egenbrøk, av samme tegn): - 13/4 = - 3 1/4 I prosent: - 13/4 = - 325 %
Hvordan skriver du en brøk som et produkt av et helt tall og en enhetsbrøk?
Regler for å finne produktet av en enhetsbrøk og et helt tall Vi skriver først hele tallet som en brøk, dvs. skriver det delt på en; for eksempel: 7 skrives som 71. Vi multipliserer deretter tellerne. Vi multipliserer nevnerne. Hvis det kreves noen forenkling, er det gjort og så skriver vi den siste brøken
Hvordan skriver du som brøk i enkleste form?
Når du skriver brøker i enkleste form, er det to regler å følge: Spør om telleren og nevneren kan deles på sammentallet, som kalles en felles faktor. Se om minst ett tall i brøken er et primenum
Hvordan skriver du noe som en funksjon?
Du skriver funksjoner med funksjonsnavnet etterfulgt av den avhengige variabelen, for eksempel f(x), g(x) eller til og med h(t) hvis funksjonen er avhengig av tid. Du leser funksjonen f(x) som 'f av x' og h(t) som 'h av t'. Funksjoner trenger ikke være lineære